Linear Regression For Machine Learning Using Python.

Welcome to the module on Linear regression in the previous blog I have explained about the “Assumptions of linear regression” and “Model Evaluation Metrics Used for Regression”.

In this section we will start with understanding the basic concept of simple linear regression and we will build a simple linear regression model in python.

The broad agenda

1. The linear regression models.
2. Residuals
3. Residual sum of squares (RSS) and R² (R-squared) (follow my previous blog)
4. Linear regression in Python.

The machine learning model can be classified into the following three types based on tasks performed and the nature of the output.

• Regression: The output variable would be a continuous variable. e.g. scores of a student
• Classification: The output variable would be a categorical variable. e.g. classifying incoming emails as spam or ham
• Clustering: No predefined notion of labels allocated to groups/clusters formed. e.g. customer segmentation

Categories of the Machine learning model

• Supervised method
  1. Regression and Classification algorithms fall under these categories.
  2. Past data with labels used for building the model.
• Unsupervised Learning
  1. The clustering algorithm falls under these categories
  2. No predefined labels are assigned to past data.

Linear Regression Intuition

Have you ever wondered? How a marketing company, could predict its sales depending on how much money they put in. Let’s say you are a fan of a particular IPL (Indian Premium League) team. And want to predict how much your team will score end of the match. And right now you are in the middle of the match, so how do you build a model how do you make this prediction?

To understand the regression lets consider company ‘X’. Where we have some previous data on marketing spending and sales there was there in the previous year. Now you want to know given that x amount of dollar or money what would be the sales.

Now the question is how you do this prediction?

Yes, you are right. You build the model and you do the prediction. As a marketing head or someone, you would have some intuition. If you increase the marketing spends you would see an increase in sales.

But then you would like to know exactly what sales you would get. And you also want to know is there any relationship between marketing spends and sales. If there is no relation between them then you would not put the money to achieves sales.

To begin with so on the x-axis, we have a marketing budget, and, on the y-axis, we have sales. And we draw a scatter plot with previous year data and you will get all these points here. It’s interesting to note on the x-axis marketing budget is correlate to sales on Y-axis. X-axis the marketing budget is also called an independent variable. And on Y-axis sales which we want to predict is the dependent variable. Here we have one independent and one dependent variable.

We called this model “Simple Linear Regression”. Where the model has only one independent variable. With the “Multi Linear Regression” model with more than one independent variable.

In simple linear regression where we try to fit a straight line that is why it’s called linear regression. A simple regression line in model attempts to explain the relationship. Between the dependent and an independent variable using a straight line.

The independent variable is also called a predictor variable. The dependent variable is an output variable.

Linear Regression Best Fit Line

What is the best straight line? Given the fact that you could have many straight lines that can fit the set of the data point.

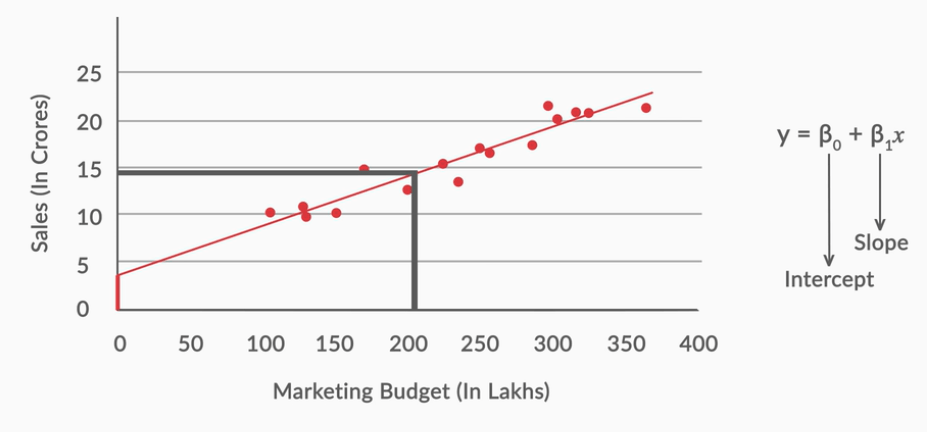
In linear regression, there is a notion of a best-fit-line, the line which fits the given scatter plot in the best way. To solve this problem in finding the best-fit-line, we use the notion called residual.

As we can see in bellow image Y=0.0528x+3.3525 which we can interpret as

Y= β₀+β₁x

This is a regression line and it’s related to the Y=mx+c straight line where β₁ is slope parameter and β₀ is the intercept parameter.

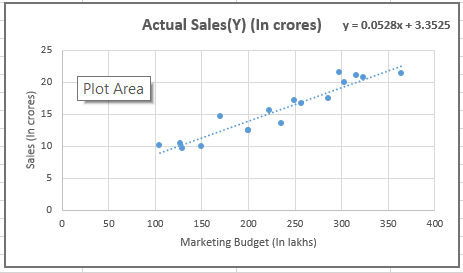
β₁ signifies if you increase the marketing budget by 1 lac what would be the impact on the y-axis sale in crores. And β₀ signifies if marketing spend is zero (0) what would be the sales.

To find the best-fit-line or regression line we have to minimize the cost function.

Residual = |predicted value — actual value|

Let’s reiterate what we have seen so far

1. We started with a scatter plot to check the relation between sales and marketing budget.
2. We found residuals and RSS for any given line passing through the scatter plot.
3. Then you found the equation of the best-fit line by minimizing the RSS and found the optimal value of β₀ and β₁.

Now we know to get the best-fit line we need to minimize a quantity called Residual Sum of Squares (RSS). So let’s understand the cost function.

Minimizing or maximizing the cost function for a particular problem. In linear regression cost, a function is the residual sum of squares (RSS).

We calculate the differentiation of the function and equate it to zero. Then we use to get 2 equations that we can solve to get β₀ and β₁ standard Math.

The other way to achieve an iterative computational approach, Gradient Descent. Gradient Descent is an optimization algorithm that optimizes the objective function. for linear regression, its cost function to reach the optimal solution.

check out the my blog An Intuition Behind Gradient Descent using Python

In Gradient Descent we start with initial parameters β₀ and β₁. And illiterate to better β₀ and β₁ such that our cost function gets minimized.

Now, we only say that. We minimize the cost function find out the best β₀ and β₁ and then use it for subsequent prediction.

Linear regression in Python.

Now let’s go back to our example. Where the marketing head, is trying to think of what could be the effect of putting his marketing budget. In three(3) different modalities, TV marketing, newspaper marketing, and radio marketing. And he wants to know how the sales would be affected by these 3 different independent variables.

In terms of our formulation, we are going to do, before that we had.

Y= β₀+β₁x

Now we have 3 different modalities TV marketing, newspaper marketing, and radio marketing. So we have a new model below, where we need to find the parameters β₀, β₁, β2, β3. I have embedded the GitHub link where you can find the implementation.

Sales = β₀+β₁*TV+ β2*newspaper + β3*radio

Linear regression implementation GitHub link

Linear Regression Analysis

I hope you guys already visit the GitHub link which I have shared. Now let’s understand the model analysis. If you see after 7th steps, optimal steps. If we are checking for p-value from the stats model, we can see that a Newspaper is insignificant.

In Step-8 we build final model with R-squared=0.893, Adj.R-squared=0.891 and Coefficient for β₁=TV=0.0455, β2 = Radio=0.1925 and β₀=2.7190

Now if we put all values together, the Sales formula we can derive as

Sales = 2.7190+ 0.0455*TV + 0.1925*radio

From the above result, we may infer. If the TV marketing budget increases by 1 unit it will affect sales by 0.045 units.
And if Radio marketing budget increases by 1 unit it will affect sales by 0.1925 units.

For practice, there is another problem statement which I have created bellow. Because it will give you proper intuition.

Linear Regression Problem Statement

A Chinese automobile company “A” Auto aspires to enter the US market. By setting up their manufacturing unit there. And producing cars in the local market to give competition to their counterparts.

They have contracted an automobile consulting company. To understand the factors on which the pricing of cars depends. They want to understand the factors affecting the pricing of cars in the American market. Since those may be very different from the Chinese market. The company wants to know:

• Which variables are significant in predicting the price of a car
• How well those variables describe the price of a car. Based on various market surveys. The consulting firm has gathered a large dataset of cars across the market.

Now you can follow the GitHub Link. for this case study, which will give you good intuition, to explore on Linear Regression.

That concludes Simple Linear Regression for now!

Footnotes:

OK, That’s it, we are done now. If you have any questions or suggestions, please feel free to reach out to me. We will come up with more Machine Learning Algorithms soon.