Welcome, to the section on ‘Logistic Regression’ for machine Learning using Python. Another technique for logistic regression for machine learning is the field of statistics. The linear regression model is used to make predictions for continuous variables (numeric variables). Logistic regression is a classification model. It will help you make predictions in cases where the output is a categorical variable.
Logistic regression is easy to interpretable for all classification models. It is very common to use various industries such as banking, healthcare, etc.
The topics that will be covered in this section are:
- Binary classification
- Sigmoid function
- Likelihood function
- Odds and log-odds
- Building a univariate logistic regression model in Python
We will look at all these concepts one by one. Also, if these terms sound a little alien to you right now, you don’t need to worry.
Univariate Logistic Regression
In this logistic regression, only one variable will be used. As we can see there is only one variable “Blood sugar level” which we need to use to classify “Diabetes“.
For example:
| Blood sugar level | Diabetes |
|---|---|
| 190 240 300 160 200 269 | No Yes Yes No Yes Yes |
Multivariate Logistic Regression
In this logistic regression for machine learning, multiple variables will be used. As we can see there are many variables to classify “Churn”.
For example:
| CustomerID | tenure | PaymentMethod | MonthlyCharges | TotalCharges | Churn | |
| 101 | 1 | Electronic | 29.85 | 29.85 | No | |
| 102 | 34 | Mailed Check | 56.95 | 1889.5 | No | |
| 103 | 2 | mailed Check | 53.85 | 108.15 | Yes | |
| 104 | 45 | Bank Transfer | 42.3 | 1840.75 | No | |
| 105 | 2 | Electronic | 70.7 | 151.65 | Yes |
Binary Classification
In the classification problems, the output is a categorical variable. for example,
- A finance company lends out a loan to a customer who wants to know if he will default or not. An email message, you want to predict Spam or ham message.
- We have an email and we want to categorize it into Primary, Social, and Promotions.
- The classification model enables us to extract a similar pattern of the data. And classify into different categories.
The classification problem where we have two possible outputs is Binary classification.
Take the example from Table 1
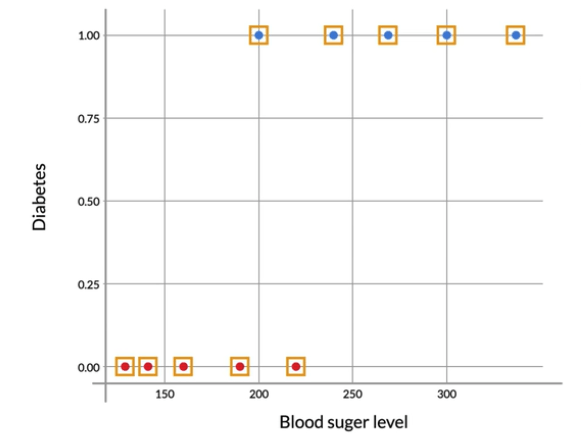
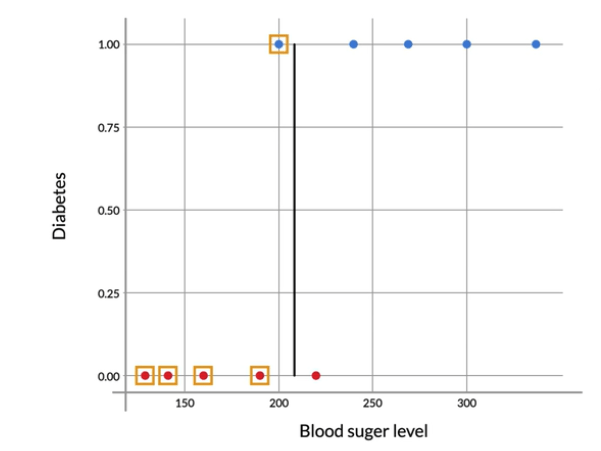

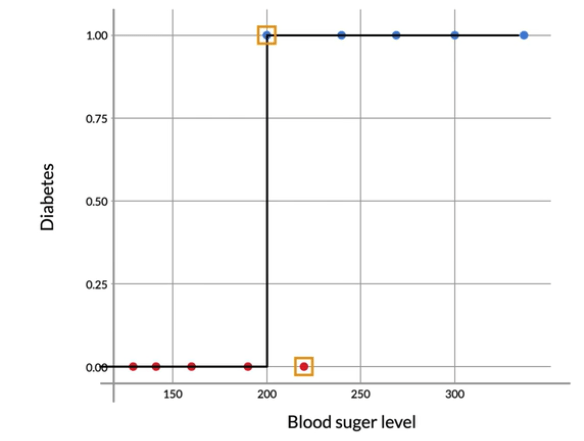
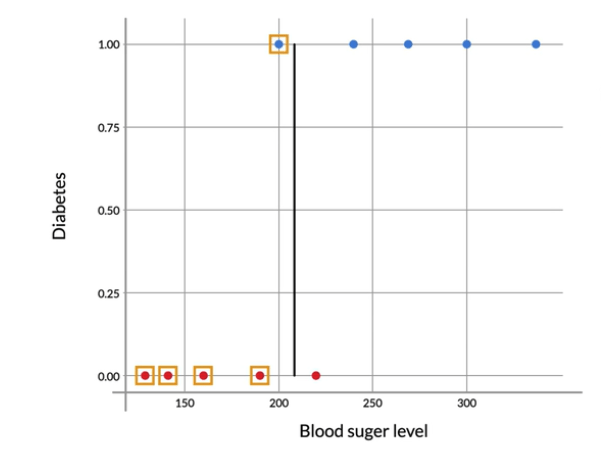
Observation
We need to predict whether a person is diabetic or not. So now we have plotted the blood sugar on the x-axis and diabetes on the y-axis. As we can see in the 1st image. The red points show non-diabetics and the blue points show diabetic persons.
We can decide based on the decision boundary as we can see in image 2 (top right). We could say that all persons with sugar levels of more the 210 are diabetics. The patient with less than 210 sugar levels is non-diabetic.
So in that case our prediction represents a curve shown in the image-3 bottom left. But there is a problem in this curve we misclassified 2 points. So now the question is, Is there a decision boundary that helps us with zero is classification? Ans is there is none.
The best case would be the one with a cutoff around 195 in image-4 (bottom right), So there would be one miss classification.
There is a problem with this approach, especially near the middle of the graph. We can not cut off based on some assumptions. It will be risky. This person’s sugar level (195 mg/dL) is very close to the threshold (200 mg/dL). Quite possible that this person was a non-diabetic with a little high blood sugar level. After all, the data does have people with little high sugar levels (220 mg/dL) (image-4), who are not diabetics.
Sigmoid Curve
We saw an example of a binary classification problem. Where a model is trying to predict whether a person has diabetes or not based on his/her blood sugar level. And we saw how using a simple boundary decision method would not work in this case.
So one way to overcome this problem of a sharp curve, is with probability.
We want the person probability of (red points) low blood sugar would be very low. And the blue point where the blood sugar level is very high, we would like to have a high probability.
And for an intermediate point where the sugar level in the range is not high and low. There we would like to have the probability close to 0.5 or 0.6.
So one possible curve, which called as a Sigmoid curve as show bellow.

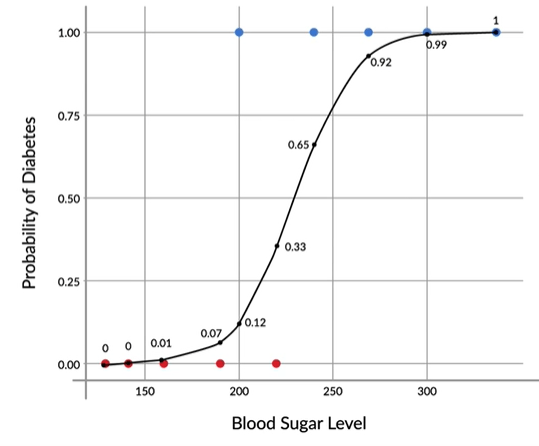
Where β0=-15 and β1=0.065
So, the Sigmoid curve has all the properties you would want. Low values at the start, high values at the end, and intermediate values in the middle. It’s a good choice for modeling the value of the probability of diabetes.
Let’s take an example.
Question: this is the sigmoid curve equation: y = p ( d i a b e t e s ) = 1 1 + e − ( β 0 + β 1 x ). here, let’s say you take β 0 = -15 and β 1 = 0.065. now, what will be the probability of diabetes for a patient with sugar level 220?
The sigmoid function is given by:
y=1 / 1 + e−(β0+β1x)
Given:
- β0=−15
- β1=0.065
- x=220 (sugar level)
We can calculate the probability of diabetes for a patient with a sugar level of 220 as follows:
y=1 / 1+e−(β0+β1x)
Substitute the given values into the equation:
y=1 / 1+e−(−15+0.065×220)
Let’s compute this step-by-step:
- Calculate the exponent term:
−15 + 0.065×220 = −0.7
- Compute e^(−0.7)
= e^−0.7≈0.4966
- Compute the final value of y:
y=11+0.4966
= 0.668y ≈ 0.668
Therefore, the probability of diabetes for a patient with a sugar level of 220 is approximately 0.668, or 66.8%.
import math
def sigmoid(beta_0, beta_1, x):
"""
This function calculates the sigmoid probability using the formula:
y = 1 / (1 + e ^ (- (beta_0 + beta_1 * x)))
Args:
beta_0: Intercept parameter of the sigmoid curve.
beta_1: Slope parameter of the sigmoid curve.
x: Input value (blood sugar level in this case).
Returns:
The probability value between 0 and 1.
"""
exponent = -(beta_0 + beta_1 * x)
return 1 / (1 + math.exp(exponent))
# Example usage with the given values
blood_sugar = 220
beta_0 = -15
beta_1 = 0.065
probability_of_diabetes = sigmoid(beta_0, beta_1, blood_sugar)
print(f"Probability of diabetes for blood sugar level {blood_sugar}: {probability_of_diabetes:.4f}")You may be wondering why can’t you fit a straight line here?
This would also have the same properties. Low values in the start, high ones towards the end, and intermediate ones in the middle.
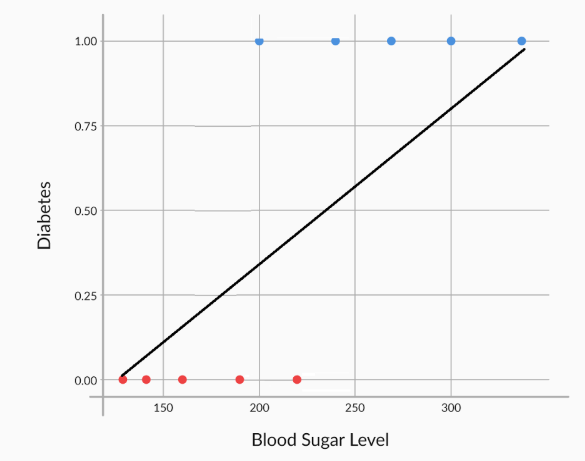
The main problem with a straight line is that it is not steep enough. In the sigmoid curve, as you can see, you have low values for a lot of points. Then the values rise suddenly, after which you have a lot of high values.
In a straight line though, the values rise from low to high very along with the line. Hence, the “boundary” region, where the probabilities transition from high to low is not present.
So, by varying the values of β0 and β1, you get different Sigmoid curves. Now, based on some function that you have to minimize or maximize, you will get the best fit Sigmoid curve.
Finding the Best Fit Sigmoid Curve
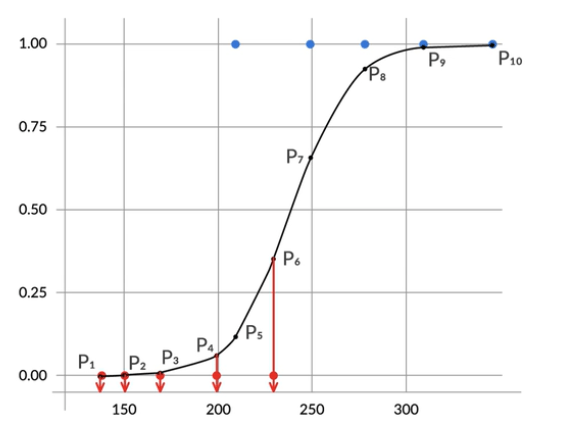
Let say we have 10 data point p1,p2,p3,p4,p5,p6,p7,p8,p9,p10 as bellow. Now let’s pick the 4th data point which is p4. We want the p4 value as small as possible.
So for the p4 value where the patient is not diabetic, we want this value to as low as possible. And for p3,p2, p1, and p6 as well (as low as possible).
Now for the other points like p5,p7,p8,p9,p10. The probability of these people being diabetics value as large as possible.
So we have 5 numbers like the lowest possible and 5 numbers which we want as the largest possible.

Likelihood function
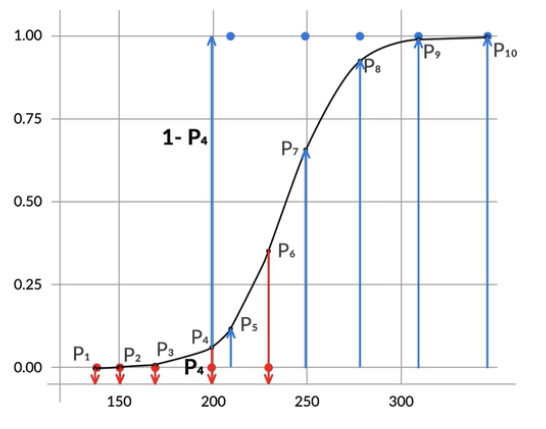
There is another way to interpret p4 value.
For example, if we say We want to minimize p4 value, at the same time we can also say we want to maximize (1-p4) value. Both interpretations are the same.
min of p4 = max of (1-p4) in probability terms.
So, we can extend this opinion and we will maximize the other value.
So, the best fitting combination of β0 and β1 will be the one which maximizes the product:
(1−P1)(1−P2)(1−P3)(1−P4)(1−P6)(P5)(P7)(P8)(P9)(P10)
This product is called the likelihood function
[(1−Pi)(1−Pi)—— for all nan-diabetics ——–] * [(Pi)(Pi) ——– for all diabetics ——-]
Odds and Log Odds
So we can manipulate the shape of the sigmoid curve with different values of β0 and β1. So far, you’ve seen this equation for logistic regression:

So this equation gives the relationship between P, the probability of diabetes, and x, the patient’s blood sugar level. But this equation is not intuitive because the relationship between P and x is so complex.
So what we need to do, simple we can simplify this equation.
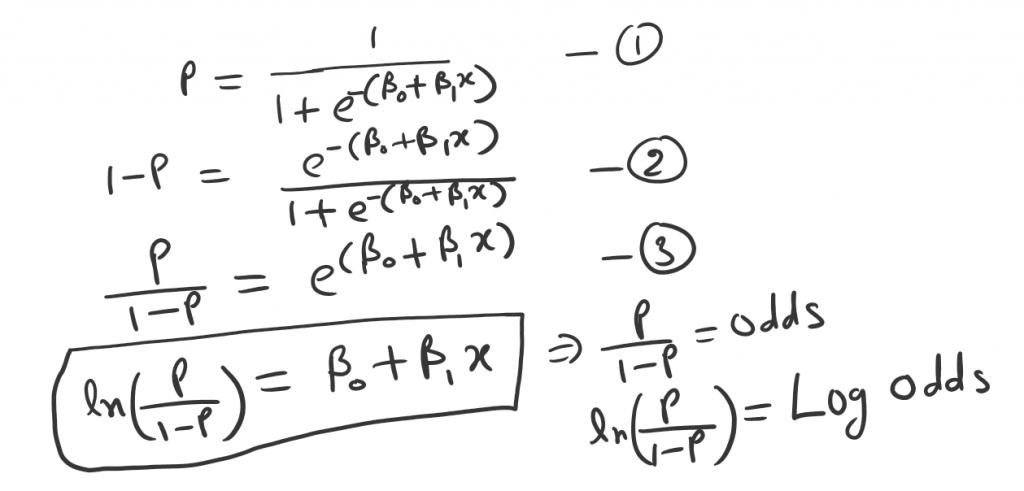
And this is indicating after taking the logs we get a nice linear form of the Sigmoid function. Where the P indicates prob of the patient is diabetics and 1-P say prob of the patient is nan-diabetics.
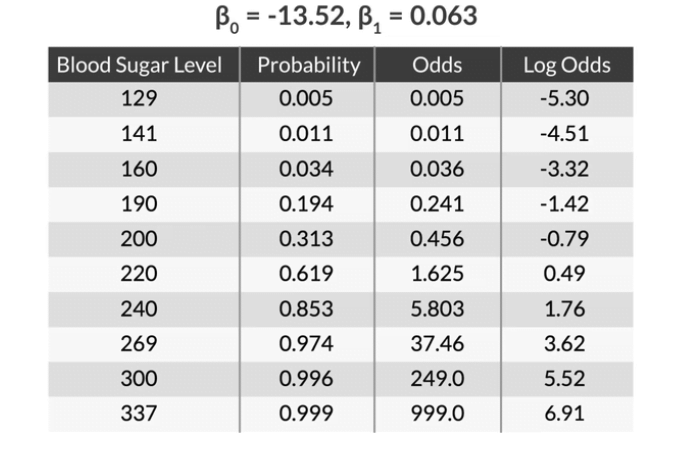
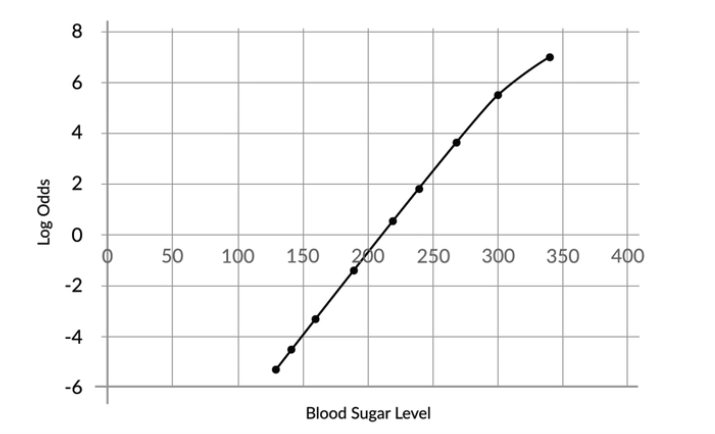
So if we have the β0=-13.52 and β1=0.063. And we can calculate the odds and log odds (left-image) of the dataset. So we can see the plot of sugar level and log odds is a straight line (β0+β1x).
Univariate Analysis in Logistic Regression for machine learning
This code is a demonstration of Univariate Logistic regression with 20 records dataset.
In Python, logistic regression implemented using Sklearn and Statsmodels libraries. Statsmodels model summary is easier using for coefficients. You can find the optimum values of β0 and β1 using this python code.
Full Source code: GitHub
In the next blog will cover the Multivariate Logistic regression. And will see how we can overcome the customer churning in Telecom industries.
Footnotes:
We saw why a simple boundary decision approach does not work very well for diabetics example. It would be too risky to decide the class boundary on the basis of the cutoff. Because, especially in the middle, the patients could belong to any class diabetic or non-diabetic.
Hence, we saw that, it is better to talk in terms of probability. One such curve which can model the probability of diabetes very well is the Sigmoid curve.
OK, that’s it, we are done now. If you have any questions or suggestions, please feel free to reach out to me. I’ll come up with more Machine Learning topic soon.

It really helped me learn the concepts. Thanks a lot.
I really appreciate you like it. I would like to thank you please share and spread to the other so they can also get benefited.